Entdecke die MINT-Rätsel

Überall in der Schule findest du QR-Codes - scanne sie und stelle dein Wissen in Mathematik, Informatik und Naturwissenschaften auf die Probe! Spannende Rätsel und knifflige Aufgaben warten auf dich. Bist du bereit, sie zu lösen? Starte 👉 hier mit dem ersten Rätsel!MINT-Woche der 26e

Wer bin ich?

In jedem Rätsel gibt es die Rubrik "Wer bin ich?", die im letzten Rätsel aufgelöst wird. Merk dir die Infos also gut.

Manche Probleme scheinen unüberwindbar – so wie die sieben Brücken von Königsberg. Doch mit der richtigen Struktur kann man Wege erkennen, die vorher unsichtbar waren. Ähnlich wie jemand, der mit Strukturen arbeitete, die das Leben selbst definieren … Wer bin ich?

Königsberger Brückenproblem

von Fabian und Leo

Rätsel

Das Königsberger Brückenproblem ist ein berühmtes mathematisches Rätsel. Es beschäftigt sich mit folgender Frage:

Ist es möglich einen Spaziergang durch die historische Stadt Königsberg so zu planen, dass man jede der sieben Brücken nur genau einmal überquert?

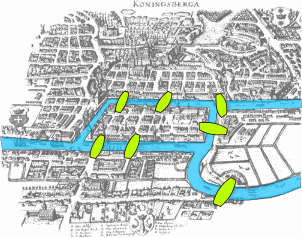Illustration Königsberg um 1730 (Brücken in Gelb)@

Bereits im 18. Jahrhundert untersuchte der Mathematiker Leonhard Euler dieses Problem und legte damit den Grundstein für ein wichtiges Gebiet der Mathematik, die Graphentheorie. Das Königsberger Brückenproblem kann man aber natürlich auch auf ähnlich aufgebaute Städte beziehen.

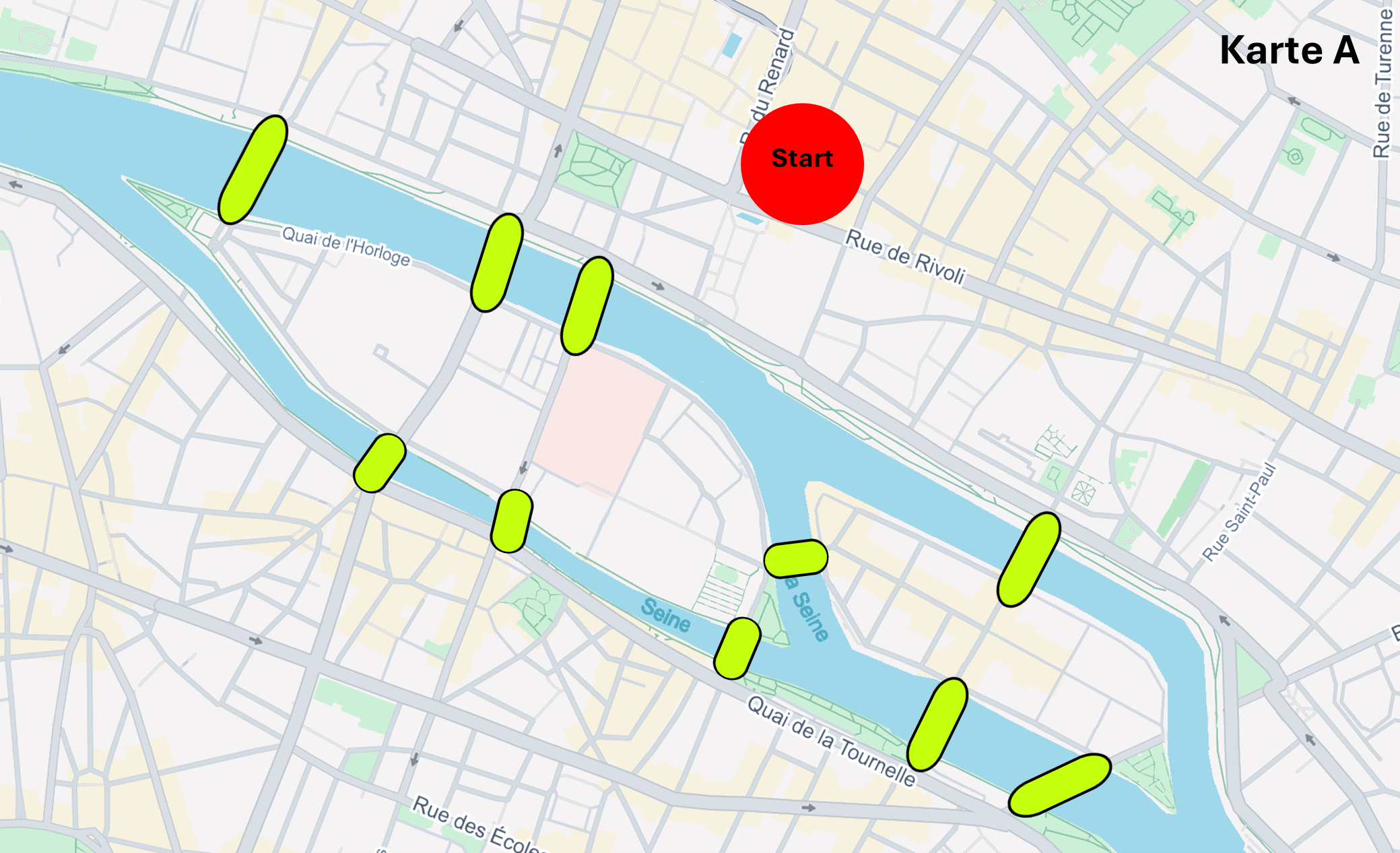
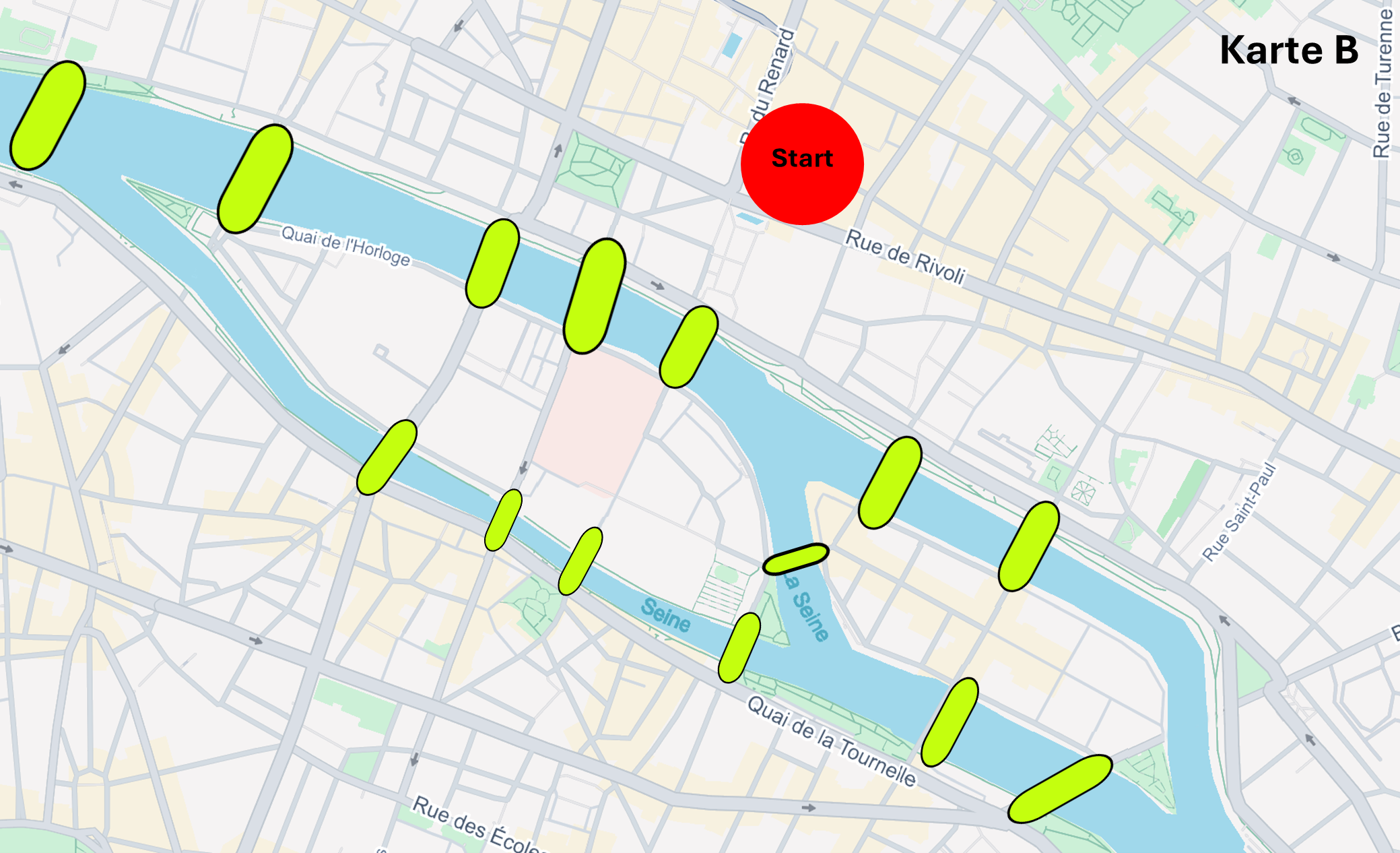
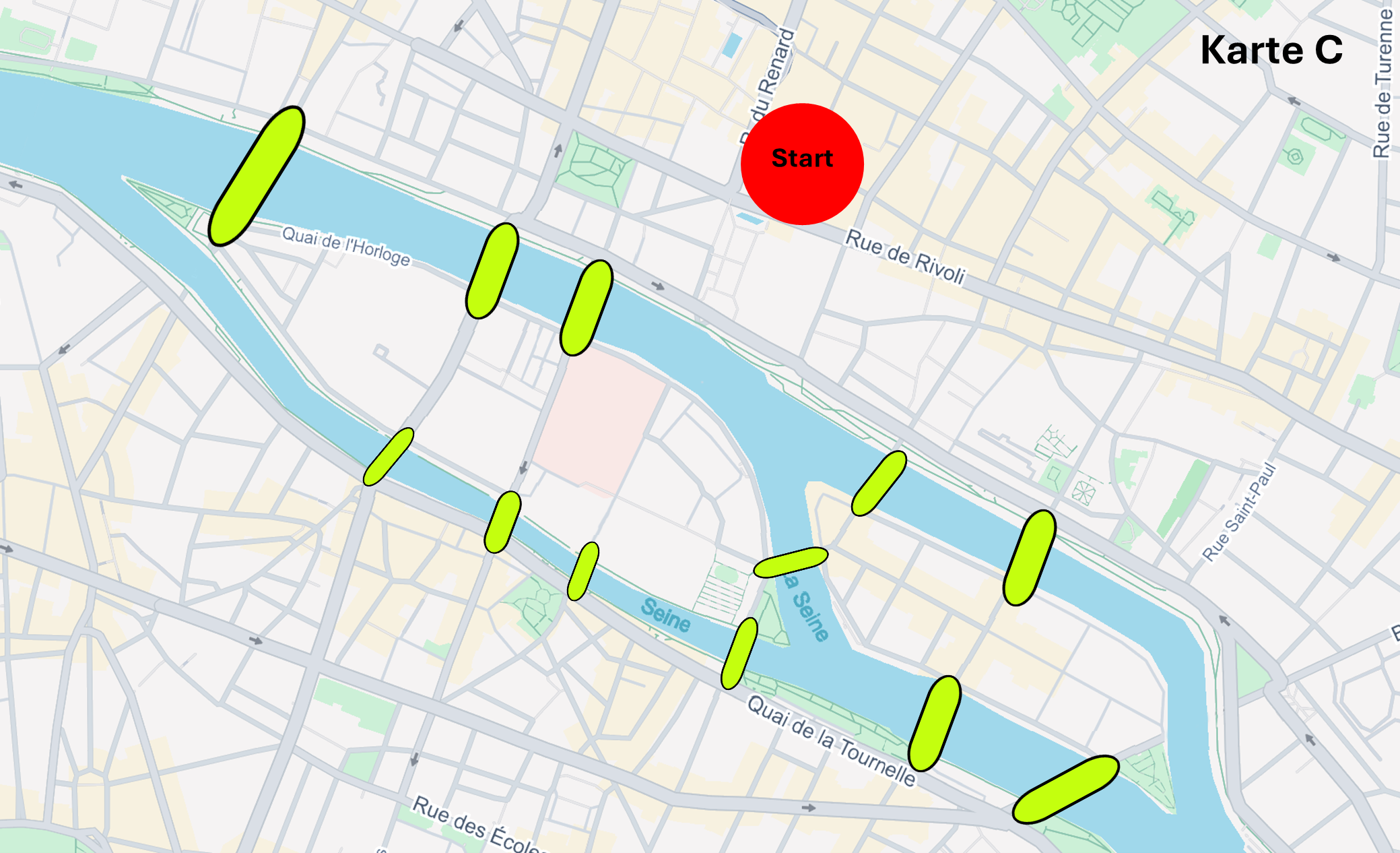
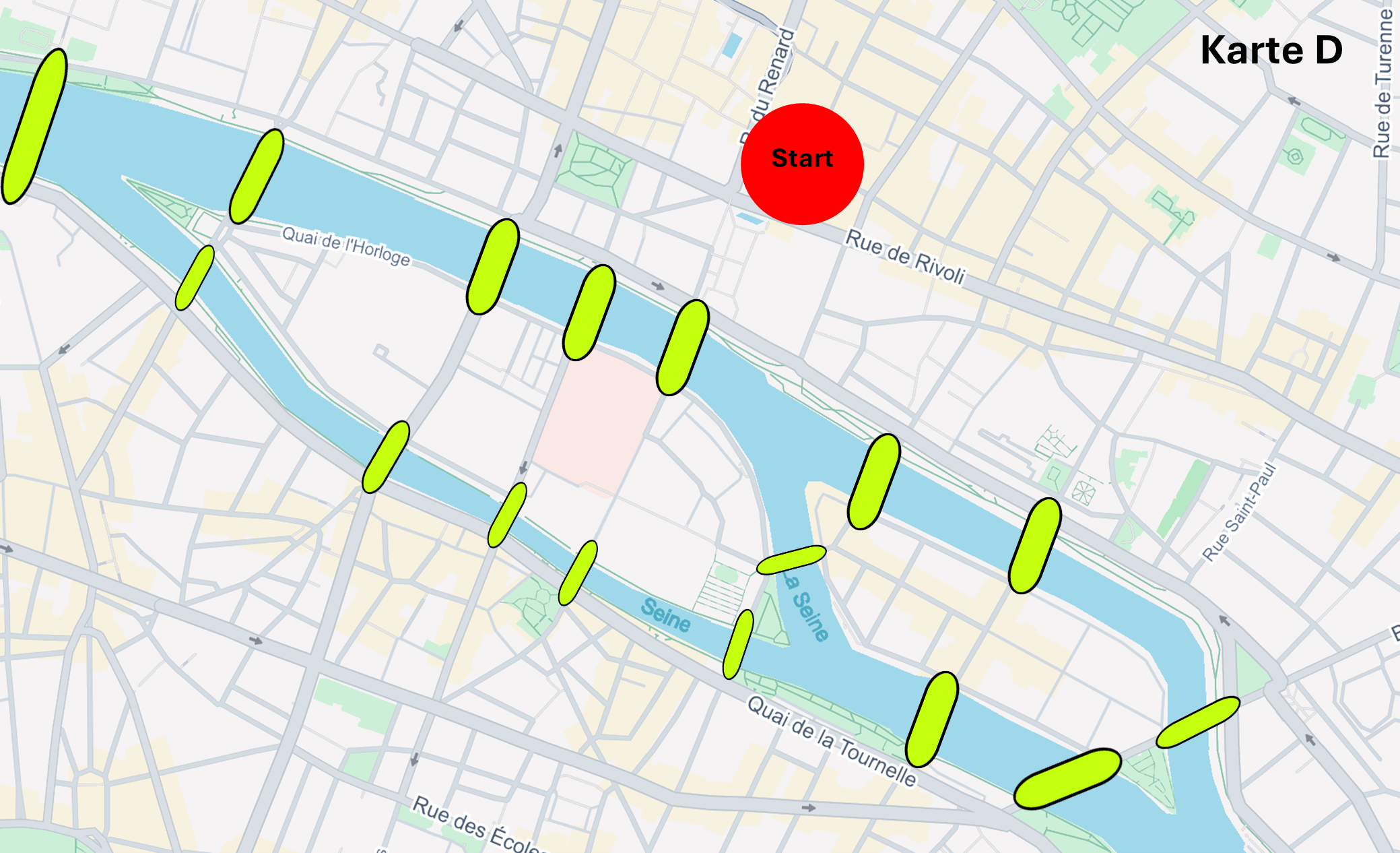
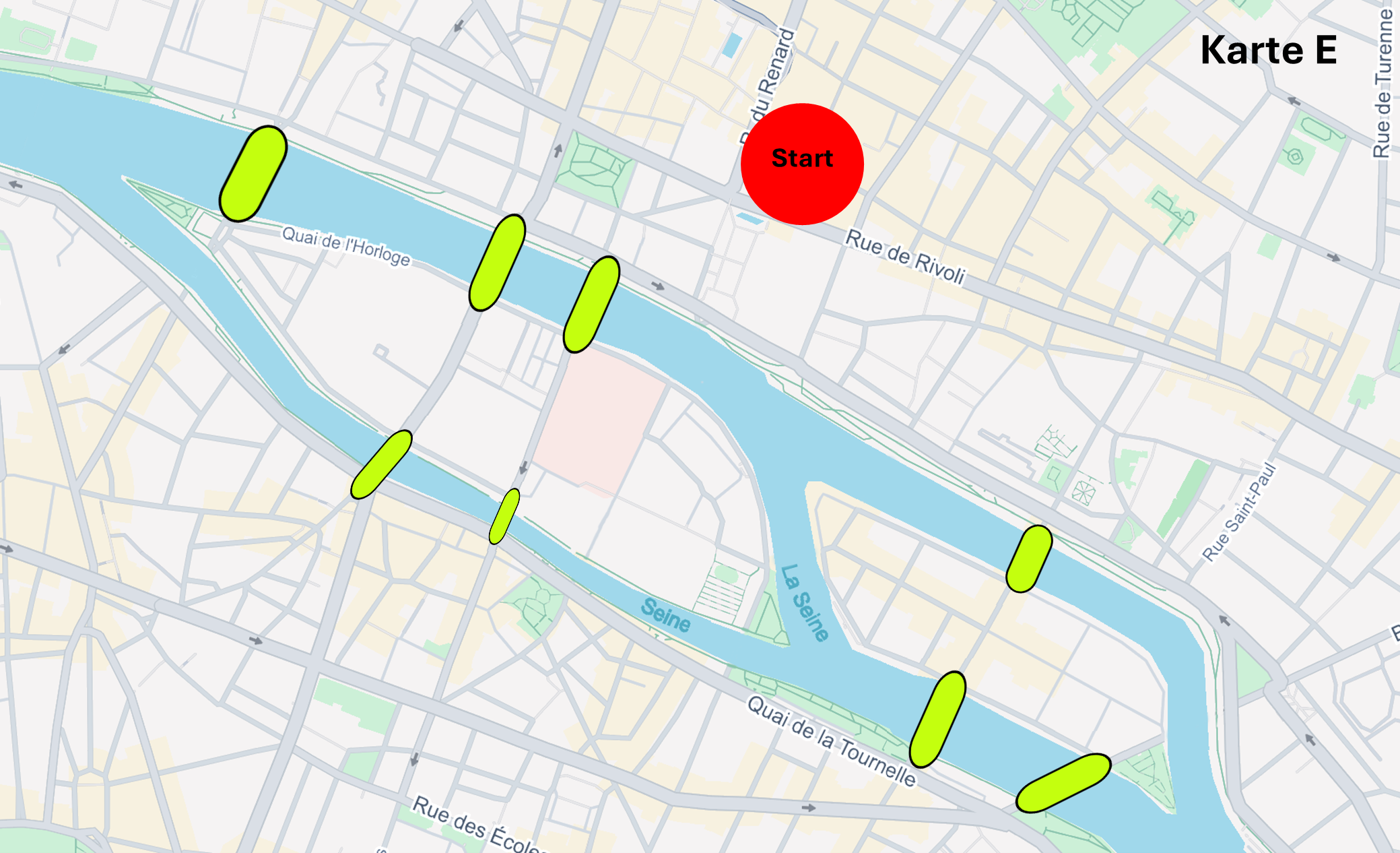
Aufgabe: Unterhalb findest du fünf Varianten eines Stadtplans der Stadt Paris, welche nur in der Anzahl der Brücken variieren. Du musst herausfinden, bei welchem der fünf Stadtpläne theoretisch ein Spaziergang möglich wäre, sodass man jede Brücke genau einmal überquert, und man schlussendlich wieder auf der gleichen Landmasse als Endpunkt angelangt (Rundgang). Wähle unterhalb die richtige Antwort A, B, C, D oder E.

(Das Wasser ist zu dreckig, da schwimmen wir nicht durch...)